The last few days we have been practising short division both with and without remainders. This has been a learning experience for EVERYONE because some of us had never seen or done short division before and others of us had done some in the past but could not recall the exact steps to complete them.
Mrs Baldwin asked us the question
Which of these numbers are divisible by… 2 … 5 … 10
In fact…
Mathematicians have developed divisibility tests for many numbers and you can use these to identify numbers, or create numbers, divisible by whatever you want.
We were each given the Divisibility test and then practiced using these tests to create some numbers.
Create a 5-digit number divisible by 3 – with no repeat digits
Create a 6 digit number divisible by 4.
Create a 5 digit number divisible by both 2 and 3
Each time we thought we discovered one we would test it by doing short division, that way we were practising this skill as well! We knew it passed the test because there would be no remainders.
Our next challenge was to place 3 digits into the boxes (no repeats) so that:
- the first digit is divisible by 1, and
- the first 2-digit number is divisible by 2, and
- the whole 3-digit number is divisible by 3
We were told that there were 115 possible solutions to this problem. So as a class we started recording our results on the board.
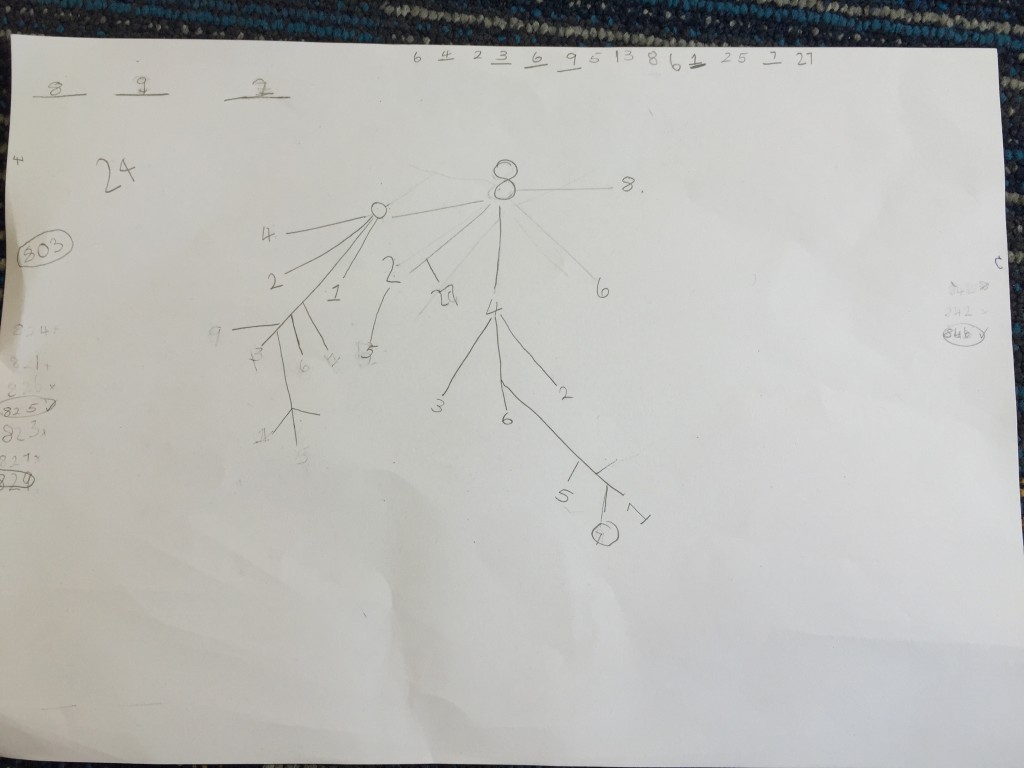
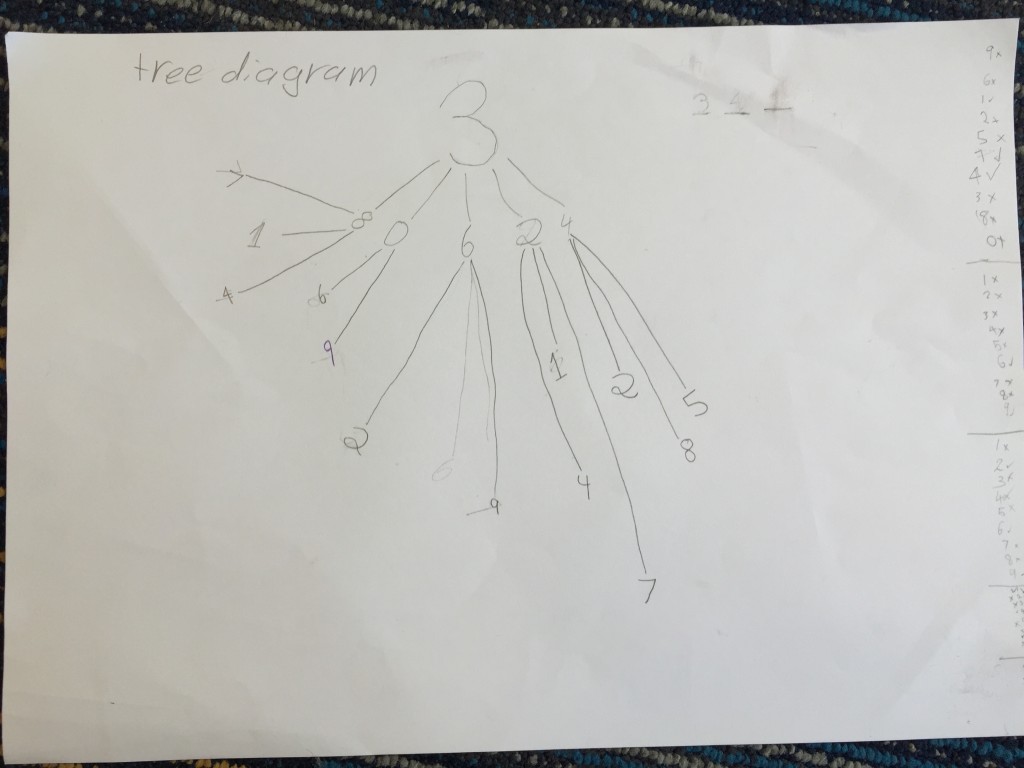
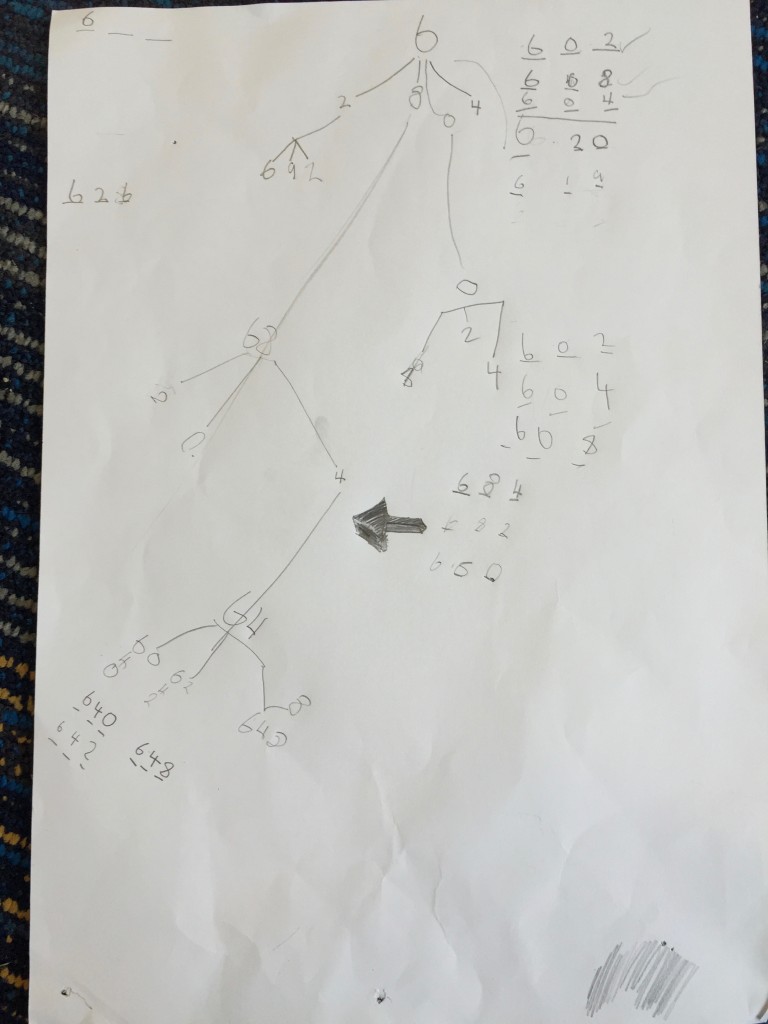
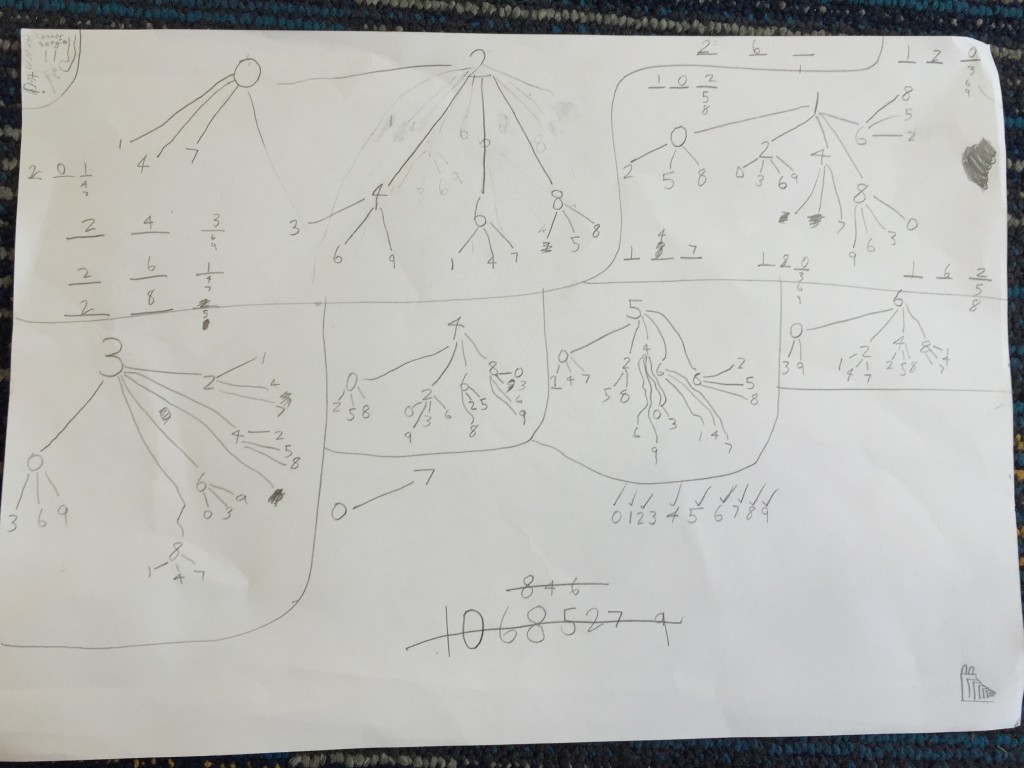
At the end of the lesson we found at least 85 possible solutions. We then talked about how good mathematicians are never convinced that all the solutions have been found unless they have a logical proof. We then used the strategy of drawing a tree diagram to help us find all possible solutions. Our class worked in groups and we each were given a number to use for the first digit to draw our tree diagrams. Here are our solutions!
We then compared these with our first round of solutions. Although there were a few we needed to fix up and change, we think for our first time recording and collating our data using the strategy of a tree diagram, we did a pretty good job!
As an extra challenge Mrs Baldwin gave us the following task:
There is a 10 digit number that passes all divisibility tests when. You need to use all the numbers from 0-9 with no repeats. There is only one solution. You need to prove your answer by showing evidence that your number passes all divisibility tests.
We have yet to have anyone in class solve this challenge! It has been wonderful to see some students really try to solve this problem and work together as a team to attempt to do this.











Howdy Miss Baldwin
What I found interesting when I was doing the tasks was learning the tree diagram because I had never seen a strategy like that before.
What I found most challenging was doing long division because I couldn’t work out what to do but I worked it out in the end.
What I think would happen is that there might more than one answer to the problem.
Just to let you know I think that I might have solved the answer to the 10 digit number.
Kind
Regards Alicia
Dear Mrs Baldwin
I think it was fun exploring new ways to divide and it was fun.
I found remembering what to do in the new strategy.
kind regards from sergio
Dear Mrs Baldwin
The thing I found most interesting was the different ways to do it and the fact that it is hard but it is great that different people do different ways.I find it hard to find the right answers for the numbers .